- ENSEMBLES (THÉORIE DES) - Théorie élémentaire
- ENSEMBLES (THÉORIE DES) - Théorie élémentaireL’algèbre des ensembles et l’étude abstraite des relations sont d’une importance croissante dans toutes les disciplines qui cherchent à s’exprimer dans un cadre rigoureux. En mathématiques, c’est l’interrogation sur les fondements de cette science, ainsi que les tentatives de formalisation des opérations logiques de la pensée qui ont conduit à l’élaboration de la théorie des ensembles; aussi cette théorie apparaît-elle comme la base de l’édifice mathématique, dont elle constitue le langage. Dans les autres sciences, et les autres domaines du savoir, les applications de l’algèbre des ensembles et de l’algèbre des propositions sont nombreuses et ne cessent d’augmenter: en physique (étude des circuits électriques, par exemple), en sciences politiques (étude des votes en vue de prendre des décisions), en sciences sociales (par exemple, problèmes d’analyse hiérarchique), etc.L’algèbre des ensembles n’est pas non plus étrangère aux progrès de la technique, ne serait-ce que parce qu’elle joue un grand rôle dans la conception et la construction des calculateurs électroniques; elle intervient aussi pour une large part dans l’organisation de l’information, les techniques de gestion, les études de marché.Parce qu’elle a une importance considérable, et aussi parce qu’elle met en évidence les opérations logiques élémentaires, la théorie des ensembles a un rôle essentiel à jouer dans la formation des esprits et intervient de plus en plus à tous les niveaux de l’enseignement. Dans l’enseignement primaire, elle est introduite à partir de manipulations de différents types de matériel conçus pour mettre en évidence les opérations qui correspondent aux mots «et» et «ou» (blocs logiques, cartes perforées; cf. enseignement des MATHÉMATIQUES). Dans le secondaire, son enseignement est devenu obligatoire, depuis 1969, à partir de la sixième. L’introduction de l’algèbre des ensembles dans l’enseignement s’accompagne généralement d’une mise à jour de la conception globale des mathématiques, ainsi que d’une évolution importante de la pédagogie, qu’on peut caractériser en deux mots, en disant qu’il ne s’agit pas d’enseigner à l’élève une science toute faite, mais de l’aider à élaborer lui-même les connaissances qu’il doit acquérir.On ne donnera pas dans cet article une construction formelle et rigoureuse de la théorie des ensembles (cf. théorie axiomatique des ENSEMBLES), mais on essayera, à partir de quelques notions premières considérées comme intuitives, d’indiquer les résultats les plus élémentaires.1. Calcul booléenLes ensemblesLeibniz, philosophe et mathématicien (1646-1716), recherche un système qui lui permette de formaliser le langage et la pensée. Pour lui, un langage formalisé doit être une pure combinaison de signes, dont seul importe l’enchaînement, de sorte qu’une machine serait capable de fournir tous les théorèmes et que toutes les controverses se résoudraient par un simple calcul.Leibniz, n’arrivant pas à exploiter toutes ses idées, dont certaines auraient pu le conduire à de meilleures conclusions, échoue dans sa tentative. Après lui, pendant tout le XVIIIe siècle et au début du XIXe, d’autres auteurs ébauchent des tentatives semblables sans arriver à avancer plus que Leibniz. À cette époque, leurs travaux, de même que ceux de Leibniz, ne sont pas connus et n’ont qu’un très faible retentissement; chacun ignore les travaux de ses prédécesseurs.C’est dans les mêmes conditions que le mathématicien anglais George Boole (1815-1864) va travailler. Boole peut être considéré comme le véritable créateur de la logique contemporaine. Son ambition est de formaliser la logique en s’inspirant des méthodes de l’analyse et de l’algèbre: «Que l’on donne des formes existantes de l’analyse une interprétation quantitative n’est que le résultat des circonstances dans lesquelles elles furent établies et ne doit pas être érigé en condition universelle de l’analyse. C’est sur le fondement de ce principe général que je me propose d’établir le calcul logique et que je lui réclame une place parmi les formes reconnues de l’analyse mathématique, sans égard au fait qu’en son objet comme en ses instruments il doive actuellement demeurer en dehors d’elle» (The Mathematical Analysis of Logic , 1847).Ce sont les travaux de Boole qui ont donné naissance à ce qu’on appelle aujourd’hui l’algèbre de Boole (ou calcul booléen), en donnant un point de départ au calcul des propositions et à l’algèbre des ensembles.Notion d’ensembleTrois mots ou symboles seront constamment utilisés dans ce qui suit: «ensemble», « élément », « 捻» (qui se lit «est élément de» ou «appartient à»). Il est impossible de définir ces mots. En effet on pourrait dire: «Un ensemble est une collection d’objets», ou encore comme Cantor (dans Gesammelte Abhanlungen ): «Par ensemble, on entend un groupement en un tout d’objets bien distincts de notre intuition ou de notre pensée.» Dans ce cas, on ne fait que déplacer le problème et il reste à définir les mots «collection», «groupement», «objets». La situation est tout à fait comparable à celle qu’on rencontre lorsqu’on veut reconstruire la géométrie; il n’est pas possible de définir les mots «point», «droite», «plan». Pour les objets correspondants, on indique leurs propriétés et les règles d’utilisation: ce sont les axiomes (cf. théorie des ENSEMBLES Théorie axiomatique des ensembles).Un ensemble est constitué d’éléments. Une image intuitive d’un ensemble est donnée par une collection d’objets, un groupement d’objets. Un élément d’un ensemble peut être soit un animal, soit un objet, soit un être mathématique, soit lui-même un ensemble. Il existe en mathématique de nombreux exemples d’ensembles d’ensembles.Dans la suite, on représentera les éléments et les ensembles par des lettres de l’alphabet. Souvent les éléments sont désignés par des lettres minuscules et les ensembles par des lettres majuscules. Rien n’oblige à respecter cette convention et cela devient impossible dans le cas des ensembles d’ensembles.
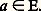 Pour exprimer que a n’est pas élément de l’ensemble E, que a n’appartient pas à l’ensemble E, on écrit:
Pour exprimer que a n’est pas élément de l’ensemble E, que a n’appartient pas à l’ensemble E, on écrit: L’expression a 殮 E est la négation de l’expression a 捻 E. Par suite, en vertu du principe du tiers exclu en logique et des relations qui existent entre une proposition et sa négation, il est possible de dire que, pour a donné et E donné, seule l’une de ces deux expressions est vraie et alors sa négation est fausse.Il faut ajouter à cela quelques règles propres à la théorie des ensembles:Règle 1. Un ensemble est parfaitement défini par la connaissance des éléments qui le constituent, ou encore: Deux ensembles sont égaux si, et seulement si, ils sont constitués par les mêmes éléments.Pour se donner un ensemble il suffit donc de se donner la liste de ses éléments. Exemples: l’ensemble constitué par les lettres a, e, i, o, u ; on le note habituellement: face=F0019 a, e, i, o, u. L’ensemble constitué par les nombres 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 sera noté de la même manière: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.Mais il y a une deuxième manière de préciser un ensemble, en les construisant à partir d’ensembles déjà connus. Ainsi, si E désigne l’ensemble des êtres humains de nationalité française et si on considère l’expression «x est inscrit sur les listes électorales», cette expression est vraie pour certains Français, fausse pour d’autres. Elle va permettre de distinguer, dans l’ensemble des Français, ceux pour lesquels cette expression est vraie, et de définir ainsi un nouvel ensemble. Cet ensemble sera noté:
L’expression a 殮 E est la négation de l’expression a 捻 E. Par suite, en vertu du principe du tiers exclu en logique et des relations qui existent entre une proposition et sa négation, il est possible de dire que, pour a donné et E donné, seule l’une de ces deux expressions est vraie et alors sa négation est fausse.Il faut ajouter à cela quelques règles propres à la théorie des ensembles:Règle 1. Un ensemble est parfaitement défini par la connaissance des éléments qui le constituent, ou encore: Deux ensembles sont égaux si, et seulement si, ils sont constitués par les mêmes éléments.Pour se donner un ensemble il suffit donc de se donner la liste de ses éléments. Exemples: l’ensemble constitué par les lettres a, e, i, o, u ; on le note habituellement: face=F0019 a, e, i, o, u. L’ensemble constitué par les nombres 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 sera noté de la même manière: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.Mais il y a une deuxième manière de préciser un ensemble, en les construisant à partir d’ensembles déjà connus. Ainsi, si E désigne l’ensemble des êtres humains de nationalité française et si on considère l’expression «x est inscrit sur les listes électorales», cette expression est vraie pour certains Français, fausse pour d’autres. Elle va permettre de distinguer, dans l’ensemble des Français, ceux pour lesquels cette expression est vraie, et de définir ainsi un nouvel ensemble. Cet ensemble sera noté: De même, dans l’ensemble A des lettres de l’alphabet français, on peut considérer celles pour qui l’expression: « 撚 est une voyelle» est vraie. On définit un ensemble noté:
De même, dans l’ensemble A des lettres de l’alphabet français, on peut considérer celles pour qui l’expression: « 撚 est une voyelle» est vraie. On définit un ensemble noté: On aurait aussi un autre ensemble:
On aurait aussi un autre ensemble: De même:
De même: Admettre qu’on peut ainsi définir des ensembles revient à admettre le principe (ou règle) suivant:Règle 2 . Quand on a un ensemble A et une propriété P, on peut définir un ensemble B dont les éléments sont les éléments de A ayant la propriété P. Si on note P(x ) l’expression «x a la propriété P», l’ensemble B peut s’écrire:
Admettre qu’on peut ainsi définir des ensembles revient à admettre le principe (ou règle) suivant:Règle 2 . Quand on a un ensemble A et une propriété P, on peut définir un ensemble B dont les éléments sont les éléments de A ayant la propriété P. Si on note P(x ) l’expression «x a la propriété P», l’ensemble B peut s’écrire: ou, en vertu de l’égalité des deux ensembles, définie par la règle 1 et qui se traduit par le signe «=»:
ou, en vertu de l’égalité des deux ensembles, définie par la règle 1 et qui se traduit par le signe «=»: Cette règle impose une définition. En effet l’ensemble B, défini ci-dessus, est tel que tous ses éléments sont des éléments de l’ensemble A. On dit que B est un sous-ensemble de A, une partie de A, ou encore que B est inclus dans A ou contenu dans A. On traduit cela par le symbole: « 說»; ainsi «B est un sous-ensemble de A» s’écrira:
Cette règle impose une définition. En effet l’ensemble B, défini ci-dessus, est tel que tous ses éléments sont des éléments de l’ensemble A. On dit que B est un sous-ensemble de A, une partie de A, ou encore que B est inclus dans A ou contenu dans A. On traduit cela par le symbole: « 說»; ainsi «B est un sous-ensemble de A» s’écrira: Une conséquence de la règle 2 est qu’à partir d’un ensemble A quelconque on peut définir un ensemble particulier, qu’on appellera l’ensemble vide , de la manière suivante: Il suffit de considérer parmi les éléments de A ceux pour lesquels la propriété «être différent d’eux-mêmes» est vraie:
Une conséquence de la règle 2 est qu’à partir d’un ensemble A quelconque on peut définir un ensemble particulier, qu’on appellera l’ensemble vide , de la manière suivante: Il suffit de considérer parmi les éléments de A ceux pour lesquels la propriété «être différent d’eux-mêmes» est vraie: On obtient ainsi un ensemble qui n’a aucun élément, appelé l’ensemble vide et noté: « 歷».Paradoxe de RussellEn 1905, Bertrand Russell montre que la notion d’«ensemble des ensembles qui ne sont pas éléments d’eux-mêmes» est contradictoire. La mise en évidence de ce résultat peut se faire de la manière suivante: à première vue les ensembles peuvent se partager en deux classes, la classe de ceux qui sont éléments d’eux-mêmes, classe de ceux pour lesquels l’expression X 捻 X est vraie; la classe de ceux qui ne sont pas éléments d’eux-mêmes, ceux pour lesquels l’expression X 捻 X est fausse ou X 殮 X est vraie. Désignons par A l’ensemble de tous les ensembles qui ne sont pas éléments d’eux-mêmes. Laquelle des deux expressions A 捻 A ou A 殮 A est-elle vraie?Supposons que A 捻 A soit vraie. Mais alors A ne peut pas être un élément de A, puisque par définition les éléments A sont des ensembles qui ne sont pas éléments d’eux-mêmes. L’expression A 殮 A doit être vraie aussi.Supposons que A 殮 A soit vraie. Mais alors, d’après la définition de A qui est constitué par les ensembles qui ne sont pas éléments d’eux-mêmes, on doit avoir A 捻 A vraie. Dans un cas comme dans l’autre, on aboutit à une contradiction. Il sera donc interdit de parler de «l’ensemble des ensembles qui ne sont pas éléments d’eux-mêmes», et, pour les mêmes raisons, de l’ensemble de tous les ensembles.Ce paradoxe est à rapprocher du paradoxe célèbre du Menteur, où le problème est de savoir si l’homme qui dit: «Je mens» dit ou non la vérité en prononçant ces paroles.Représentation graphiqueIl est souvent commode de représenter un élément par un point du plan, et un ensemble par l’intérieur d’une courbe fermée. Ainsi la figure 1 représente un ensemble A, a n’est pas élément de A, b et c sont éléments de A.Les sous-ensembles sont alors représentés comme des portions de l’ensemble. Ainsi B est une partie ou sous-ensemble de A. Ce sont les diagrammes de Venn.Lewis Carroll propose une présentation analogue, mais l’ensemble A est représenté par un rectangle, un sous-ensemble B étant obtenu par partage du rectangle en deux par un segment de droite. Cette présentation a l’avantage de conserver une symétrie entre le sous-ensemble B et le sous-ensemble complémentaire B constitué par les éléments de A qui ne sont pas dans B (fig. 1).De toute manière, ces représentations ne sont que des images, et il y a au moins autant de différence entre ces images et les êtres mathématiques qu’elles représentent qu’entre un schéma et l’objet représenté par ce schéma ou qu’entre l’écriture d’un mot en français et la signification de ce mot. Mais de même que les schémas permettent de se représenter les objets et servent à penser et à raisonner, de même les figures proposées ci-dessus peuvent apporter une aide importante aux raisonnements.Ensemble des parties d’un ensembleUn ensemble A est partie ou sous-ensemble de E si tous les éléments de A sont des éléments de E.Pour un ensemble E ayant trois éléments désignés par a , b , c , il est facile d’énumérer toutes ses parties. Il y a d’abord E lui-même, qui répond à la condition ci-dessus: E 說 E. Ensuite les parties ayant deux éléments, ce sont: face=F0019 a, b, a, c, b, c. Ensuite les parties ayant un élément: face=F0019 a, b, c. Enfin la partie vide: face=F0019 歷. Il est facile de voir que l’ensemble vide est une partie de E soit en remarquant qu’il vérifie la définition ci-dessus, soit en remarquant qu’il peut être défini de la manière suivante:
On obtient ainsi un ensemble qui n’a aucun élément, appelé l’ensemble vide et noté: « 歷».Paradoxe de RussellEn 1905, Bertrand Russell montre que la notion d’«ensemble des ensembles qui ne sont pas éléments d’eux-mêmes» est contradictoire. La mise en évidence de ce résultat peut se faire de la manière suivante: à première vue les ensembles peuvent se partager en deux classes, la classe de ceux qui sont éléments d’eux-mêmes, classe de ceux pour lesquels l’expression X 捻 X est vraie; la classe de ceux qui ne sont pas éléments d’eux-mêmes, ceux pour lesquels l’expression X 捻 X est fausse ou X 殮 X est vraie. Désignons par A l’ensemble de tous les ensembles qui ne sont pas éléments d’eux-mêmes. Laquelle des deux expressions A 捻 A ou A 殮 A est-elle vraie?Supposons que A 捻 A soit vraie. Mais alors A ne peut pas être un élément de A, puisque par définition les éléments A sont des ensembles qui ne sont pas éléments d’eux-mêmes. L’expression A 殮 A doit être vraie aussi.Supposons que A 殮 A soit vraie. Mais alors, d’après la définition de A qui est constitué par les ensembles qui ne sont pas éléments d’eux-mêmes, on doit avoir A 捻 A vraie. Dans un cas comme dans l’autre, on aboutit à une contradiction. Il sera donc interdit de parler de «l’ensemble des ensembles qui ne sont pas éléments d’eux-mêmes», et, pour les mêmes raisons, de l’ensemble de tous les ensembles.Ce paradoxe est à rapprocher du paradoxe célèbre du Menteur, où le problème est de savoir si l’homme qui dit: «Je mens» dit ou non la vérité en prononçant ces paroles.Représentation graphiqueIl est souvent commode de représenter un élément par un point du plan, et un ensemble par l’intérieur d’une courbe fermée. Ainsi la figure 1 représente un ensemble A, a n’est pas élément de A, b et c sont éléments de A.Les sous-ensembles sont alors représentés comme des portions de l’ensemble. Ainsi B est une partie ou sous-ensemble de A. Ce sont les diagrammes de Venn.Lewis Carroll propose une présentation analogue, mais l’ensemble A est représenté par un rectangle, un sous-ensemble B étant obtenu par partage du rectangle en deux par un segment de droite. Cette présentation a l’avantage de conserver une symétrie entre le sous-ensemble B et le sous-ensemble complémentaire B constitué par les éléments de A qui ne sont pas dans B (fig. 1).De toute manière, ces représentations ne sont que des images, et il y a au moins autant de différence entre ces images et les êtres mathématiques qu’elles représentent qu’entre un schéma et l’objet représenté par ce schéma ou qu’entre l’écriture d’un mot en français et la signification de ce mot. Mais de même que les schémas permettent de se représenter les objets et servent à penser et à raisonner, de même les figures proposées ci-dessus peuvent apporter une aide importante aux raisonnements.Ensemble des parties d’un ensembleUn ensemble A est partie ou sous-ensemble de E si tous les éléments de A sont des éléments de E.Pour un ensemble E ayant trois éléments désignés par a , b , c , il est facile d’énumérer toutes ses parties. Il y a d’abord E lui-même, qui répond à la condition ci-dessus: E 說 E. Ensuite les parties ayant deux éléments, ce sont: face=F0019 a, b, a, c, b, c. Ensuite les parties ayant un élément: face=F0019 a, b, c. Enfin la partie vide: face=F0019 歷. Il est facile de voir que l’ensemble vide est une partie de E soit en remarquant qu’il vérifie la définition ci-dessus, soit en remarquant qu’il peut être défini de la manière suivante: L’ensemble des parties de E sera donc un ensemble de 8 éléments:
L’ensemble des parties de E sera donc un ensemble de 8 éléments: Pour un ensemble quelconque E, on peut être amené à considérer des parties de E et l’ensemble des parties de E. Nous admettrons l’existence de ce nouvel ensemble, dont la définition pourrait être: L’ensemble des parties d’un ensemble E est un ensemble dont les éléments sont les sous-ensembles ou parties de E. Cet ensemble est noté: face=F0021 戮 (E). Ainsi:
Pour un ensemble quelconque E, on peut être amené à considérer des parties de E et l’ensemble des parties de E. Nous admettrons l’existence de ce nouvel ensemble, dont la définition pourrait être: L’ensemble des parties d’un ensemble E est un ensemble dont les éléments sont les sous-ensembles ou parties de E. Cet ensemble est noté: face=F0021 戮 (E). Ainsi: Pour l’ensemble a, b, c, on aura:
Pour l’ensemble a, b, c, on aura: De même:
De même: Si l’ensemble E a un élément, 戮 (E) a deux éléments; si E a deux éléments, 戮 (E) en a quatre; si E a trois éléments, 戮 (E) en a huit; on peut généraliser et voir que si l’ensemble E a n éléments, l’ensemble 戮 (E) en a 2n . Cette règle peut apparaître à l’aide d’un arbre de choix tel que celui qui est représenté sur la figure 2 dans le cas d’un ensemble à trois éléments: a , b , c.On voit ici que, chaque fois qu’on ajoute un élément, il y aura dédoublement, donc multiplication par 2 du nombre d’éléments. On démontre alors le résultat par récurrence.On peut aussi organiser l’ensemble des parties d’un ensemble sur un schéma en reliant deux parties par une flèche lorsqu’on passe de l’une à l’autre par adjonction d’un élément à la première (fig. 3). Ainsi, si l’ensemble a un seul élément a , il a deux parties: face=F0019 歷 et a. Pour E = a, b, on trouve quatre parties: face=F0019 歷, a, b, a, b; remarquons qu’on passe des deux premières aux deux dernières par adjonction de l’élément b. Pour E = a, b, c, on aurait un schéma, obtenu par dédoublement du précédent.On pourrait continuer ainsi pour des ensembles à 4, 5, 6, ... éléments. On a ici un schéma de l’organisation par la relation «est sous-ensemble de» de l’ensemble des parties d’un ensemble, une partie étant sous-ensemble d’une autre s’il existe un chemin dans le sens des flèches allant de la première à la deuxième (cf. ensembles ORDONNÉS).Algèbre des ensemblesPour ce qui suit, il est commode de supposer donné un ensemble E et de ne considérer que des sous-ensembles de E, donc des éléments de 戮 (E). On appelle quelquefois référentiel cet ensemble fixe auquel on se réfère. Cela permet de définir des opérations dans 戮 (E): intersection, union, etc.Intersection de deux ensemblesSi A et B sont deux ensembles, il peut être commode dans certains cas de considérer l’ensemble des éléments communs. Ainsi, dans l’ensemble des Français, si A désigne l’ensemble des Français inscrits sur les listes électorales en 1970 et si B désigne l’ensemble des Français habitant la ville de Paris pendant l’année 1970, il peut être intéressant, dans certains cas, de pouvoir considérer l’ensemble des Français inscrits sur les listes électorales et habitant la ville de Paris en 1970. Un tel ensemble, constitué par les éléments communs à l’ensemble A et à l’ensemble B, sera appelé l’intersection de A et de B. On le note A 惡 B, ce qui se lit «intersection de A et de B».Ainsi, si, dans l’ensemble des mots français, A désigne l’ensemble des mots dont la première lettre est un «a», B désigne l’ensemble des mots dont la dernière lettre est un «p», A 惡 B désigne alors l’ensemble des mots dont la première lettre est un «a» et la dernière est un «p».On peut donner une définition formelle de l’intersection:
Si l’ensemble E a un élément, 戮 (E) a deux éléments; si E a deux éléments, 戮 (E) en a quatre; si E a trois éléments, 戮 (E) en a huit; on peut généraliser et voir que si l’ensemble E a n éléments, l’ensemble 戮 (E) en a 2n . Cette règle peut apparaître à l’aide d’un arbre de choix tel que celui qui est représenté sur la figure 2 dans le cas d’un ensemble à trois éléments: a , b , c.On voit ici que, chaque fois qu’on ajoute un élément, il y aura dédoublement, donc multiplication par 2 du nombre d’éléments. On démontre alors le résultat par récurrence.On peut aussi organiser l’ensemble des parties d’un ensemble sur un schéma en reliant deux parties par une flèche lorsqu’on passe de l’une à l’autre par adjonction d’un élément à la première (fig. 3). Ainsi, si l’ensemble a un seul élément a , il a deux parties: face=F0019 歷 et a. Pour E = a, b, on trouve quatre parties: face=F0019 歷, a, b, a, b; remarquons qu’on passe des deux premières aux deux dernières par adjonction de l’élément b. Pour E = a, b, c, on aurait un schéma, obtenu par dédoublement du précédent.On pourrait continuer ainsi pour des ensembles à 4, 5, 6, ... éléments. On a ici un schéma de l’organisation par la relation «est sous-ensemble de» de l’ensemble des parties d’un ensemble, une partie étant sous-ensemble d’une autre s’il existe un chemin dans le sens des flèches allant de la première à la deuxième (cf. ensembles ORDONNÉS).Algèbre des ensemblesPour ce qui suit, il est commode de supposer donné un ensemble E et de ne considérer que des sous-ensembles de E, donc des éléments de 戮 (E). On appelle quelquefois référentiel cet ensemble fixe auquel on se réfère. Cela permet de définir des opérations dans 戮 (E): intersection, union, etc.Intersection de deux ensemblesSi A et B sont deux ensembles, il peut être commode dans certains cas de considérer l’ensemble des éléments communs. Ainsi, dans l’ensemble des Français, si A désigne l’ensemble des Français inscrits sur les listes électorales en 1970 et si B désigne l’ensemble des Français habitant la ville de Paris pendant l’année 1970, il peut être intéressant, dans certains cas, de pouvoir considérer l’ensemble des Français inscrits sur les listes électorales et habitant la ville de Paris en 1970. Un tel ensemble, constitué par les éléments communs à l’ensemble A et à l’ensemble B, sera appelé l’intersection de A et de B. On le note A 惡 B, ce qui se lit «intersection de A et de B».Ainsi, si, dans l’ensemble des mots français, A désigne l’ensemble des mots dont la première lettre est un «a», B désigne l’ensemble des mots dont la dernière lettre est un «p», A 惡 B désigne alors l’ensemble des mots dont la première lettre est un «a» et la dernière est un «p».On peut donner une définition formelle de l’intersection: L’intersection de A et de B est l’ensemble des éléments de E qui sont éléments de A et éléments de B (fig. 4). Dans cette définition, un mot est important, c’est le mot «et». La définition est fondée sur la conjonction de deux propriétés: l’appartenance à A, l’appartenance à B. Toutes les propriétés de l’intersection sont des traductions, en langage des ensembles, des propriétés du mot «et» dans le langage courant et en logique des propositions.Voici un autre exemple d’intersection:
L’intersection de A et de B est l’ensemble des éléments de E qui sont éléments de A et éléments de B (fig. 4). Dans cette définition, un mot est important, c’est le mot «et». La définition est fondée sur la conjonction de deux propriétés: l’appartenance à A, l’appartenance à B. Toutes les propriétés de l’intersection sont des traductions, en langage des ensembles, des propriétés du mot «et» dans le langage courant et en logique des propositions.Voici un autre exemple d’intersection: où A est l’ensemble des diviseurs de 18, B est l’ensemble des diviseurs de 45, et A 惡 B est l’ensemble des diviseurs communs à 18 et à 45.Dans le cas où l’intersection de A et de B est l’ensemble vide, on dit que A et B sont disjoints.Parmi les propriétés de l’intersection, on peut signaler:
où A est l’ensemble des diviseurs de 18, B est l’ensemble des diviseurs de 45, et A 惡 B est l’ensemble des diviseurs communs à 18 et à 45.Dans le cas où l’intersection de A et de B est l’ensemble vide, on dit que A et B sont disjoints.Parmi les propriétés de l’intersection, on peut signaler: i.e. l’intersection de A et de B est un sous-ensemble de A et un sous-ensemble de B; c’est aussi un sous-ensemble de tout ensemble contenant A ou B comme sous-ensemble.
i.e. l’intersection de A et de B est un sous-ensemble de A et un sous-ensemble de B; c’est aussi un sous-ensemble de tout ensemble contenant A ou B comme sous-ensemble. i.e. l’intersection de A et de B est égale à l’intersection de B et de A, ce qui tient au fait qu’il revient au même de dire que «x est élément de A et élément de B» ou de dire que «x est élément de B et élément de A».
i.e. l’intersection de A et de B est égale à l’intersection de B et de A, ce qui tient au fait qu’il revient au même de dire que «x est élément de A et élément de B» ou de dire que «x est élément de B et élément de A». cela veut dire que l’intersection de A 惡 B avec C donne le même résultat que l’intersection de A avec B 惡 C. L’ordre dans lequel on effectue l’opération intersection n’a pas d’influence sur le résultat, ce qui permet de supprimer les parenthèses dans l’écriture:
cela veut dire que l’intersection de A 惡 B avec C donne le même résultat que l’intersection de A avec B 惡 C. L’ordre dans lequel on effectue l’opération intersection n’a pas d’influence sur le résultat, ce qui permet de supprimer les parenthèses dans l’écriture: Cette propriété est à rapprocher de celle du mot «et» dans le langage courant; en effet, il revient au même de dire: «est élément de A et de B, et est aussi élément de C» que de dire «est élément de A et est élément de B et de C».
Cette propriété est à rapprocher de celle du mot «et» dans le langage courant; en effet, il revient au même de dire: «est élément de A et de B, et est aussi élément de C» que de dire «est élément de A et est élément de B et de C». i.e. l’intersection de A avec A est A lui-même.
i.e. l’intersection de A avec A est A lui-même. i.e. l’intersection de A avec l’ensemble vide est l’ensemble vide.
i.e. l’intersection de A avec l’ensemble vide est l’ensemble vide. i.e. l’intersection de A et B est égale à A si, et seulement si, A est un sous-ensemble de B.
i.e. l’intersection de A et B est égale à A si, et seulement si, A est un sous-ensemble de B. i.e. tout sous-ensemble commun à A et B est un sous-ensemble de leur intersection et réciproquement.Réunion de deux sous-ensemblesSi A et B sont deux ensembles, il peut être intéressant, dans certains cas, de «réunir» leurs éléments en un ensemble global. Ainsi, si A désigne l’ensemble des Français possédant une voiture et B l’ensemble des Français possédant un appartement, on peut avoir à considérer l’ensemble des Français qui ont une voiture ou un appartement. Ce nouvel ensemble sera appelé la réunion de A et de B.La réunion de deux ensembles A et B est un ensemble constitué par les éléments qui appartiennent à A ou à B. On note «A 聆 B» ce nouvel ensemble. «A 聆 B» se lit «union de A et de B», ou encore «A union B» (fig. 5).La définition formelle peut s’écrire:
i.e. tout sous-ensemble commun à A et B est un sous-ensemble de leur intersection et réciproquement.Réunion de deux sous-ensemblesSi A et B sont deux ensembles, il peut être intéressant, dans certains cas, de «réunir» leurs éléments en un ensemble global. Ainsi, si A désigne l’ensemble des Français possédant une voiture et B l’ensemble des Français possédant un appartement, on peut avoir à considérer l’ensemble des Français qui ont une voiture ou un appartement. Ce nouvel ensemble sera appelé la réunion de A et de B.La réunion de deux ensembles A et B est un ensemble constitué par les éléments qui appartiennent à A ou à B. On note «A 聆 B» ce nouvel ensemble. «A 聆 B» se lit «union de A et de B», ou encore «A union B» (fig. 5).La définition formelle peut s’écrire: Dans cette définition, le mot «ou» joue un rôle très important et toutes les propriétés de la réunion sont des traductions, en langage des ensembles, des propriétés du mot «ou» au sens non disjonctif dans le langage courant et en logique des propositions.Voici un exemple de réunion:
Dans cette définition, le mot «ou» joue un rôle très important et toutes les propriétés de la réunion sont des traductions, en langage des ensembles, des propriétés du mot «ou» au sens non disjonctif dans le langage courant et en logique des propositions.Voici un exemple de réunion: Parmi les propriétés de la réunion, il faut signaler:
Parmi les propriétés de la réunion, il faut signaler: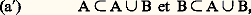 i.e. A et B sont des sous-ensembles de la réunion A 聆 B.
i.e. A et B sont des sous-ensembles de la réunion A 聆 B. i.e. la réunion de A et de B est égale à la réunion de B et de A, car il revient au même de dire que «x est élément de A ou de B» et de dire que «x est élément de B ou de A».
i.e. la réunion de A et de B est égale à la réunion de B et de A, car il revient au même de dire que «x est élément de A ou de B» et de dire que «x est élément de B ou de A». i.e. la réunion de A 聆 B avec C donne le même résultat que la réunion de A avec B 聆 C. L’ordre dans lequel on effectue les réunions n’a pas d’influence sur le résultat; on peut donc supprimer les parenthèses dans l’écriture:
i.e. la réunion de A 聆 B avec C donne le même résultat que la réunion de A avec B 聆 C. L’ordre dans lequel on effectue les réunions n’a pas d’influence sur le résultat; on peut donc supprimer les parenthèses dans l’écriture: On pourrait rapprocher cette propriété de celle du mot «ou» dans le langage courant.
On pourrait rapprocher cette propriété de celle du mot «ou» dans le langage courant. i.e. la réunion de A avec A est A.
i.e. la réunion de A avec A est A. i.e. la réunion de A avec l’ensemble vide est A lui-même.
i.e. la réunion de A avec l’ensemble vide est A lui-même. i.e. la réunion de A et de B est égale à B si, et seulement si, A est un sous-ensemble de B.
i.e. la réunion de A et de B est égale à B si, et seulement si, A est un sous-ensemble de B. i.e. A et B sont sous-ensembles d’un ensemble D si, et seulement si, la réunion de A et de B est un sous-ensemble de D.Enfin deux propriétés de distributivité, faisant intervenir la réunion et l’intersection sont à signaler (fig. 6):
i.e. A et B sont sous-ensembles d’un ensemble D si, et seulement si, la réunion de A et de B est un sous-ensemble de D.Enfin deux propriétés de distributivité, faisant intervenir la réunion et l’intersection sont à signaler (fig. 6): ComplémentaireTous les ensembles considérés ici sont des parties d’un même ensemble E. On peut remarquer que chaque fois que l’on définit une partie de E, on définit automatiquement une autre partie de E, celle qui est constituée par les éléments de E qui ne sont pas dans la première. Ainsi, dans l’ensemble des Français, en définissant l’ensemble des Français inscrits sur les listes électorales, on définit en même temps l’ensemble des Français qui ne sont pas inscrits sur les listes électorales.On appelle complémentaire d’un ensemble A, sous-ensemble de E, l’ensemble constitué par les éléments de E qui ne sont pas dans A (fig. 7). On note «A» ou « 璉A» le complémentaire de A. On peut écrire:
ComplémentaireTous les ensembles considérés ici sont des parties d’un même ensemble E. On peut remarquer que chaque fois que l’on définit une partie de E, on définit automatiquement une autre partie de E, celle qui est constituée par les éléments de E qui ne sont pas dans la première. Ainsi, dans l’ensemble des Français, en définissant l’ensemble des Français inscrits sur les listes électorales, on définit en même temps l’ensemble des Français qui ne sont pas inscrits sur les listes électorales.On appelle complémentaire d’un ensemble A, sous-ensemble de E, l’ensemble constitué par les éléments de E qui ne sont pas dans A (fig. 7). On note «A» ou « 璉A» le complémentaire de A. On peut écrire: Quand on parle de complémentaire, il est très important de bien préciser l’ensemble de référence E. Évidemment, le complémentaire de A est un sous-ensemble de E. Entre les parties d’un ensemble E, la complémentarité établit une correspondance un à un, une application bijective (cf. Propriétés des applications in chap. 2) de l’ensemble 戮 (E) dans lui-même.Le complémentaire étant défini à partir de la négation, négation de la proposition «appartient à A», ses propriétés sont la traduction, en langage des ensembles, de celles de la négation.
Quand on parle de complémentaire, il est très important de bien préciser l’ensemble de référence E. Évidemment, le complémentaire de A est un sous-ensemble de E. Entre les parties d’un ensemble E, la complémentarité établit une correspondance un à un, une application bijective (cf. Propriétés des applications in chap. 2) de l’ensemble 戮 (E) dans lui-même.Le complémentaire étant défini à partir de la négation, négation de la proposition «appartient à A», ses propriétés sont la traduction, en langage des ensembles, de celles de la négation. i.e. le complémentaire du complémentaire de A est A lui-même.
i.e. le complémentaire du complémentaire de A est A lui-même. i.e. le complémentaire de l’ensemble vide est l’ensemble E, et le complémentaire de l’ensemble E est l’ensemble vide.
i.e. le complémentaire de l’ensemble vide est l’ensemble E, et le complémentaire de l’ensemble E est l’ensemble vide. i.e. l’intersection de A et de son complémentaire est vide, et la réunion de A et de son complémentaire est l’ensemble E. Cela constitue une propriété caractéristique du complémentaire et aurait pu être pris comme définition.
i.e. l’intersection de A et de son complémentaire est vide, et la réunion de A et de son complémentaire est l’ensemble E. Cela constitue une propriété caractéristique du complémentaire et aurait pu être pris comme définition. i.e. A est un sous-ensemble de B si, et seulement si, le complémentaire de B est un sous-ensemble du complémentaire de A.Les lois de Morgan:
i.e. A est un sous-ensemble de B si, et seulement si, le complémentaire de B est un sous-ensemble du complémentaire de A.Les lois de Morgan: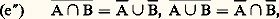 expriment (fig. 8 et 9) que le complémentaire de l’intersection de deux ensembles est égal à la réunion des complémentaires de ces deux ensembles, et le complémentaire de la réunion de deux ensembles est égal à l’intersection des complémentaires de ces deux ensembles.Autres opérationsOn peut définir d’autres opérations entre les parties d’un ensemble. Ainsi la différence A – B de deux ensembles A et B est l’ensemble constitué par les éléments de A qui ne sont pas éléments de B (fig. 10).On remarque facilement que:
expriment (fig. 8 et 9) que le complémentaire de l’intersection de deux ensembles est égal à la réunion des complémentaires de ces deux ensembles, et le complémentaire de la réunion de deux ensembles est égal à l’intersection des complémentaires de ces deux ensembles.Autres opérationsOn peut définir d’autres opérations entre les parties d’un ensemble. Ainsi la différence A – B de deux ensembles A et B est l’ensemble constitué par les éléments de A qui ne sont pas éléments de B (fig. 10).On remarque facilement que: La différence symétrique de deux ensembles A et B est un ensemble constitué par les éléments de A qui ne sont pas dans B et les éléments de B qui ne sont pas dans A (fig. 11). On le notera A 蓮 B, dans ce qui suit.On peut vérifier les égalités:
La différence symétrique de deux ensembles A et B est un ensemble constitué par les éléments de A qui ne sont pas dans B et les éléments de B qui ne sont pas dans A (fig. 11). On le notera A 蓮 B, dans ce qui suit.On peut vérifier les égalités: Algèbre et anneau de BooleL’ensemble 戮 (E) des parties d’un ensemble muni des opérations d’union et d’intersection et de la complémentarité constitue ce qu’on appelle une algèbre de Boole. En effet, les propriétés suivantes sont vérifiées:a ) Les opérations d’union et d’intersection sont associatives:
Algèbre et anneau de BooleL’ensemble 戮 (E) des parties d’un ensemble muni des opérations d’union et d’intersection et de la complémentarité constitue ce qu’on appelle une algèbre de Boole. En effet, les propriétés suivantes sont vérifiées:a ) Les opérations d’union et d’intersection sont associatives: et commutatives:
et commutatives: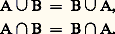 b ) Il y a un élément neutre pour chacune des deux opérations: pour l’union, 歷 est élément neutre, car quel que soit l’ensemble A on a: A 聆 歷 = A; et, pour l’intersection, E est élément neutre, car quel que soit A dans 戮 (E), on a: A 惡 E = A.c ) Chacune des deux opérations est distributive par rapport à l’autre:
b ) Il y a un élément neutre pour chacune des deux opérations: pour l’union, 歷 est élément neutre, car quel que soit l’ensemble A on a: A 聆 歷 = A; et, pour l’intersection, E est élément neutre, car quel que soit A dans 戮 (E), on a: A 惡 E = A.c ) Chacune des deux opérations est distributive par rapport à l’autre: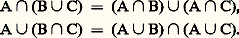 d ) Le complémentaire A 漣 de A vérifie les deux propriétés: A 聆 A 漣 = E (élément neutre de l’intersection), et A 惡 A 漣 = 歷 (élément neutre de la réunion).Si maintenant on considère l’ensemble 戮(E) muni des opérations de différence symétrique et d’intersection, il a une structure d’anneau de Boole. En effet, la différence symétrique donne une structure de groupe commutatif à 戮(E); l’opération intersection donne alors à 戮(E) une structure d’anneau booléen [cf. ANNEAUX ET ALGÈBRES].Fonctions caractéristiquesIl est commode de présenter les opérations entre parties d’un ensemble en utilisant les fonctions caractéristiques. Si A est une partie de E, la fonction caractéristique de l’ensemble A est une fonction qui à chaque élément de E associe 1 si cet élément est dans A et 0 si cet élément n’est pas dans A.Lorsqu’on a la fonction caractéristique d’une partie A de E, il est facile de déterminer celle du complémentaire A 漣 de A. Il suffit de changer les 0 en 1 et les 1 en 0. Il est aussi facile de voir si un ensemble est inclus dans un autre: on voit que B est inclus dans A si, chaque fois que la fonction caractéristique de B a la valeur 1, celle de A l’a aussi. Les éléments de l’intersection de A et de B sont ceux pour lesquels les fonctions caractéristiques de A et de B prennent ensemble la valeur 1. La fonction caractéristique de A 惡 B est donc facile à construire. Il en est de même pour celle de A 聆 B.Tout cela peut s’interpréter autrement. En effet, considérons l’ensemble X ayant deux éléments 0, 1 et définissons sur cet ensemble deux opérations.La première opération sera notée + et sera définie par:
d ) Le complémentaire A 漣 de A vérifie les deux propriétés: A 聆 A 漣 = E (élément neutre de l’intersection), et A 惡 A 漣 = 歷 (élément neutre de la réunion).Si maintenant on considère l’ensemble 戮(E) muni des opérations de différence symétrique et d’intersection, il a une structure d’anneau de Boole. En effet, la différence symétrique donne une structure de groupe commutatif à 戮(E); l’opération intersection donne alors à 戮(E) une structure d’anneau booléen [cf. ANNEAUX ET ALGÈBRES].Fonctions caractéristiquesIl est commode de présenter les opérations entre parties d’un ensemble en utilisant les fonctions caractéristiques. Si A est une partie de E, la fonction caractéristique de l’ensemble A est une fonction qui à chaque élément de E associe 1 si cet élément est dans A et 0 si cet élément n’est pas dans A.Lorsqu’on a la fonction caractéristique d’une partie A de E, il est facile de déterminer celle du complémentaire A 漣 de A. Il suffit de changer les 0 en 1 et les 1 en 0. Il est aussi facile de voir si un ensemble est inclus dans un autre: on voit que B est inclus dans A si, chaque fois que la fonction caractéristique de B a la valeur 1, celle de A l’a aussi. Les éléments de l’intersection de A et de B sont ceux pour lesquels les fonctions caractéristiques de A et de B prennent ensemble la valeur 1. La fonction caractéristique de A 惡 B est donc facile à construire. Il en est de même pour celle de A 聆 B.Tout cela peut s’interpréter autrement. En effet, considérons l’ensemble X ayant deux éléments 0, 1 et définissons sur cet ensemble deux opérations.La première opération sera notée + et sera définie par: La deuxième opération sera notée . et sera définie par:
La deuxième opération sera notée . et sera définie par: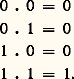 Cet ensemble X muni des deux opérations + et 練 définies ci-dessus constitue ce qu’on appelle une algèbre de Boole, c’est l’anneau Z/(2) des entiers relatifs modulo 2. Il joue un rôle fondamental en logique des propositions. En effet, si on interprète 1 comme le «vrai» et 0 comme le «faux», valeur qu’on peut attribuer aux propositions, les opérations + et 練 sont alors la disjonction (ou) la conjonction (et) des propositions. Enfin la complémentarité qui est ici l’échange de 0 en 1 et de 1 en 0 s’interprète comme une négation.Les fonctions caractéristiques sont alors des fonctions qui prennent leur valeur dans l’ensemble X, et si on désigne par f A la fonction caractéristique de A on a:
Cet ensemble X muni des deux opérations + et 練 définies ci-dessus constitue ce qu’on appelle une algèbre de Boole, c’est l’anneau Z/(2) des entiers relatifs modulo 2. Il joue un rôle fondamental en logique des propositions. En effet, si on interprète 1 comme le «vrai» et 0 comme le «faux», valeur qu’on peut attribuer aux propositions, les opérations + et 練 sont alors la disjonction (ou) la conjonction (et) des propositions. Enfin la complémentarité qui est ici l’échange de 0 en 1 et de 1 en 0 s’interprète comme une négation.Les fonctions caractéristiques sont alors des fonctions qui prennent leur valeur dans l’ensemble X, et si on désigne par f A la fonction caractéristique de A on a: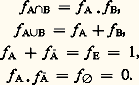 Remarquons que la formule:
Remarquons que la formule: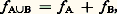 ne serait pas vraie si on définissait l’addition des nombres au sens usuel; on aurait alors f A size=1聆B = f A + f B 漣 f A f B.Partition d’un ensembleLorsqu’on a un ensemble d’objets ayant chacun une couleur bien déterminée, on peut être amené à les classer suivant leur couleur. On effectue ainsi une classification des objets, chaque objet étant dans une classe et une seule. On a de la sorte une image de ce que le mathématicien appelle une partition.Une partition d’un ensemble est un ensemble de parties non vides de cet ensemble tel que deux parties distinctes n’aient pas d’élément commun et que chaque élément de l’ensemble soit dans une de ces parties. C’est en quelque sorte l’ensemble des classes d’une classification.Ainsi, dans l’ensemble des entiers naturels N = 1, 2, 3, 4, ..., on peut constituer une partition en trois classes en plaçant dans la première classe les nombres divisibles par 3, dans la deuxième ceux dont le reste de la division par 3 est 1, dans la troisième ceux dont le reste est 2. Ainsi chaque nombre est rangé dans une classe et aucun ne se trouve dans deux classes en même temps. Les classes sont alors: face=F0019 0, 3, 6, 9, 12, 15, ..., 1, 4, 7, 10, ... et 2, 5, 8, 11, ....On trouve de nombreux exemples de partitions dans les problèmes de rangement, les dépouillements de questionnaires, les classifications, etc.Quelques applicationsCircuits électriquesL’algèbre de Boole étudiée ci-dessus, ou algèbre des parties d’un ensemble, peut être appliquée à l’étude des circuits électriques. Ainsi, dans un circuit relié aux deux pôles d’une pile par exemple, si on place un interrupteur à deux positions, deux cas peuvent se présenter: ou bien l’interrupteur est fermé et le courant passe, on peut noter cela par 1; ou bien l’interrupteur est ouvert et le courant ne passe pas, on peut noter ceci par 0. On peut alors définir des opérations sur les interrupteurs analogues à celle que nous avions dans l’ensemble X = 0,1 ci-dessus.Deux interrupteurs I et J disposés en série ne laissent passer le courant que s’ils sont fermés tous les deux. Notons I 練 J cette combinaison en série des deux interrupteurs I et J; l’état de I . J est alors défini par la table:De même, si deux interrupteurs sont placés en parallèle, le courant passe dès que l’un ou l’autre des interrupteurs est fermé. Si on note I + J l’état du circuit, I + J est défini à partir de I et de J comme l’indique le tableau suivant:Enfin on peut retrouver la négation par un circuit complémentaire. I 漣, le tableau donnant l’état de chacun des circuits I et I 漣:Cela peut permettre d’étudier les circuits électriques, mais, réciproquement, c’est ce qui a permis l’utilisation des circuits électriques dans les machines à calculer électroniques.Information analogiqueL’information analogique décrite mathématiquement par des fonctions continues (signal électrique issu d’un microphone) doit être quantifiée et codée pour être traitée par les procédés de l’électronique moderne utilisant largement les microprocesseurs et le traitement numérique de l’information.Le principe de la quantification est le suivant. Au signal analogique est associé un nombre d’états possibles selon le graphe suivant:Le nombre d’états possibles de quantification est en général élevé, 212 par exemple. Le traitement numérique impose d’associer à chaque état de quantification une suite de valeurs booléennes (12 variables booléennes peuvent être utilisées); l’information est alors représentée par une suite d’états 0 ou 1.Une application connue de tous est le disque compact; celui-ci permet de stocker les suites binaires sous forme de «trous» situés sur le sillon du disque suivant le schéma figurant dans la figure 25 de l’article ENREGISTREMENT. Le nombre de 0 et de 1 stockés sur le disque compact est très élevé: 3 000 mégaéléments binaires!L’évolution est loin d’être terminée: les images sont stockables en utilisant le même procédé, et l’on attend beaucoup de la logique floue (fondements mathématiques dérivés de l’algèbre de Boole, mais différents) et des réseaux de neurones.2. RelationsProduit cartésienLe coupleSoit E et F deux ensembles. Pour x 捻 E et y 捻 F, on introduit un nouvel objet mathématique, le couple de premier terme x et de second terme y , défini par le symbole:
ne serait pas vraie si on définissait l’addition des nombres au sens usuel; on aurait alors f A size=1聆B = f A + f B 漣 f A f B.Partition d’un ensembleLorsqu’on a un ensemble d’objets ayant chacun une couleur bien déterminée, on peut être amené à les classer suivant leur couleur. On effectue ainsi une classification des objets, chaque objet étant dans une classe et une seule. On a de la sorte une image de ce que le mathématicien appelle une partition.Une partition d’un ensemble est un ensemble de parties non vides de cet ensemble tel que deux parties distinctes n’aient pas d’élément commun et que chaque élément de l’ensemble soit dans une de ces parties. C’est en quelque sorte l’ensemble des classes d’une classification.Ainsi, dans l’ensemble des entiers naturels N = 1, 2, 3, 4, ..., on peut constituer une partition en trois classes en plaçant dans la première classe les nombres divisibles par 3, dans la deuxième ceux dont le reste de la division par 3 est 1, dans la troisième ceux dont le reste est 2. Ainsi chaque nombre est rangé dans une classe et aucun ne se trouve dans deux classes en même temps. Les classes sont alors: face=F0019 0, 3, 6, 9, 12, 15, ..., 1, 4, 7, 10, ... et 2, 5, 8, 11, ....On trouve de nombreux exemples de partitions dans les problèmes de rangement, les dépouillements de questionnaires, les classifications, etc.Quelques applicationsCircuits électriquesL’algèbre de Boole étudiée ci-dessus, ou algèbre des parties d’un ensemble, peut être appliquée à l’étude des circuits électriques. Ainsi, dans un circuit relié aux deux pôles d’une pile par exemple, si on place un interrupteur à deux positions, deux cas peuvent se présenter: ou bien l’interrupteur est fermé et le courant passe, on peut noter cela par 1; ou bien l’interrupteur est ouvert et le courant ne passe pas, on peut noter ceci par 0. On peut alors définir des opérations sur les interrupteurs analogues à celle que nous avions dans l’ensemble X = 0,1 ci-dessus.Deux interrupteurs I et J disposés en série ne laissent passer le courant que s’ils sont fermés tous les deux. Notons I 練 J cette combinaison en série des deux interrupteurs I et J; l’état de I . J est alors défini par la table:De même, si deux interrupteurs sont placés en parallèle, le courant passe dès que l’un ou l’autre des interrupteurs est fermé. Si on note I + J l’état du circuit, I + J est défini à partir de I et de J comme l’indique le tableau suivant:Enfin on peut retrouver la négation par un circuit complémentaire. I 漣, le tableau donnant l’état de chacun des circuits I et I 漣:Cela peut permettre d’étudier les circuits électriques, mais, réciproquement, c’est ce qui a permis l’utilisation des circuits électriques dans les machines à calculer électroniques.Information analogiqueL’information analogique décrite mathématiquement par des fonctions continues (signal électrique issu d’un microphone) doit être quantifiée et codée pour être traitée par les procédés de l’électronique moderne utilisant largement les microprocesseurs et le traitement numérique de l’information.Le principe de la quantification est le suivant. Au signal analogique est associé un nombre d’états possibles selon le graphe suivant:Le nombre d’états possibles de quantification est en général élevé, 212 par exemple. Le traitement numérique impose d’associer à chaque état de quantification une suite de valeurs booléennes (12 variables booléennes peuvent être utilisées); l’information est alors représentée par une suite d’états 0 ou 1.Une application connue de tous est le disque compact; celui-ci permet de stocker les suites binaires sous forme de «trous» situés sur le sillon du disque suivant le schéma figurant dans la figure 25 de l’article ENREGISTREMENT. Le nombre de 0 et de 1 stockés sur le disque compact est très élevé: 3 000 mégaéléments binaires!L’évolution est loin d’être terminée: les images sont stockables en utilisant le même procédé, et l’on attend beaucoup de la logique floue (fondements mathématiques dérivés de l’algèbre de Boole, mais différents) et des réseaux de neurones.2. RelationsProduit cartésienLe coupleSoit E et F deux ensembles. Pour x 捻 E et y 捻 F, on introduit un nouvel objet mathématique, le couple de premier terme x et de second terme y , défini par le symbole: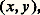 avec la convention que:
avec la convention que: On appelle produit cartésien de deux ensembles E et F, noté E 憐 F, l’ensemble des couples ayant pour premier terme un élément de E et pour second terme un élément de F. Par exemple, si E =a , b , c et F =A, B sont des ensembles à trois et deux éléments respectivement, l’ensemble E 憐 F a six éléments qui sont:
On appelle produit cartésien de deux ensembles E et F, noté E 憐 F, l’ensemble des couples ayant pour premier terme un élément de E et pour second terme un élément de F. Par exemple, si E =a , b , c et F =A, B sont des ensembles à trois et deux éléments respectivement, l’ensemble E 憐 F a six éléments qui sont: et l’ensemble E 憐 E a neuf éléments qui sont:
et l’ensemble E 憐 E a neuf éléments qui sont: plus généralement, si E et F sont des ensembles finis contenant m et n éléments, le produit cartésien E 憐 F est fini et contient mn éléments.Justifions la terminologie de cartésien. Le choix de deux axes de coordonnées dans le plan de la géométrie élémentaire permet d’identifier l’ensemble des points du plan à l’ensemble R 憐 R = R2 des couples de nombres réels, au point M correspondant le couple ayant pour premier terme l’abscisse de M et pour second terme son ordonnée; c’est le principe de la géométrie analytique de Descartes, chez qui apparaît pour la première fois la notion mathématique de couple.De nos jours, on définit souvent ainsi le plan de la géométrie élémentaire; dans ce qui suit, cette identification sera toujours faite.Représentations graphiquesOn représente souvent (représentation dite cartésienne) un ensemble produit E 憐 F par l’ensemble des points d’un rectangle (surtout ne pas confondre avec les diagrammes de Carroll!), les ensembles E et F étant représentés par deux côtés perpendiculaires de ce rectangle (fig. 13); un sous-ensemble A de E 憐 F est alors représenté par un sous-ensemble de ce rectangle.Dans le cas d’ensembles finis, on peut faire le tableau donnant les éléments de l’ensemble produit ou utiliser une représentation par des points du plan (cf. fig. 14 pour l’exemple ci-dessus). Pour représenter les sous-ensembles, on peut indiquer leurs éléments sur la représentation, mais on peut aussi utiliser la représentation sagittale, dont voici le principe: on représente le couple (x , y ) par deux points (appelés x et y ) réunis par une flèche allant de x vers y ; dans le cas particulier d’un couple (x , x ), on dessine une boucle fermée allant de x à x. Sur la figure 15, on donne les représentations cartésienne et sagittale du sous-ensemble:
plus généralement, si E et F sont des ensembles finis contenant m et n éléments, le produit cartésien E 憐 F est fini et contient mn éléments.Justifions la terminologie de cartésien. Le choix de deux axes de coordonnées dans le plan de la géométrie élémentaire permet d’identifier l’ensemble des points du plan à l’ensemble R 憐 R = R2 des couples de nombres réels, au point M correspondant le couple ayant pour premier terme l’abscisse de M et pour second terme son ordonnée; c’est le principe de la géométrie analytique de Descartes, chez qui apparaît pour la première fois la notion mathématique de couple.De nos jours, on définit souvent ainsi le plan de la géométrie élémentaire; dans ce qui suit, cette identification sera toujours faite.Représentations graphiquesOn représente souvent (représentation dite cartésienne) un ensemble produit E 憐 F par l’ensemble des points d’un rectangle (surtout ne pas confondre avec les diagrammes de Carroll!), les ensembles E et F étant représentés par deux côtés perpendiculaires de ce rectangle (fig. 13); un sous-ensemble A de E 憐 F est alors représenté par un sous-ensemble de ce rectangle.Dans le cas d’ensembles finis, on peut faire le tableau donnant les éléments de l’ensemble produit ou utiliser une représentation par des points du plan (cf. fig. 14 pour l’exemple ci-dessus). Pour représenter les sous-ensembles, on peut indiquer leurs éléments sur la représentation, mais on peut aussi utiliser la représentation sagittale, dont voici le principe: on représente le couple (x , y ) par deux points (appelés x et y ) réunis par une flèche allant de x vers y ; dans le cas particulier d’un couple (x , x ), on dessine une boucle fermée allant de x à x. Sur la figure 15, on donne les représentations cartésienne et sagittale du sous-ensemble: de l’ensemble E 憐 F vu ci-dessus.Relations binairesSoit E et F des ensembles. Une relation de source E et but F est une propriété sur l’ensemble produit E 憐 F, c’est-à-dire une propriété des couples (x , y ), x 捻 E et y 捻 F. Ainsi une relation définit un sous-ensemble de E 憐 F, appelé son graphe , formé des couples pour lesquels la relation est vraie (cf. chap. 1). Réciproquement, tout sous-ensemble A 說 E 憐 F définit une relation de source E et de but F, à savoir la propriété:
de l’ensemble E 憐 F vu ci-dessus.Relations binairesSoit E et F des ensembles. Une relation de source E et but F est une propriété sur l’ensemble produit E 憐 F, c’est-à-dire une propriété des couples (x , y ), x 捻 E et y 捻 F. Ainsi une relation définit un sous-ensemble de E 憐 F, appelé son graphe , formé des couples pour lesquels la relation est vraie (cf. chap. 1). Réciproquement, tout sous-ensemble A 說 E 憐 F définit une relation de source E et de but F, à savoir la propriété: du couple (x , y ). Lorsque F = E, on dit qu’on a une relation sur E. Si une relation 倫 est vraie pour le couple (x , y ), on écrira souvent x 倫 y .Exemples(1) Sur un ensemble E, la relation d’égalité «x = y » a pour graphe l’ensemble des couples (x , x), x 捻 E; cet ensemble est appelé la diagonale de l’ensemble E 憐 E.(2) Prenons pour E l’ensemble des quatre voyellesa , e , i , o et pour F l’ensemble des quatre premiers chiffres1, 2, 3, 4; la figure 16 indique les représentations cartésienne et sagittale de la relation «la voyelle x figure dans l’écriture en langue française du chiffre y ». Par exemple (a , 4) appartient au graphe (car a est dans qua tre), mais (a , 3) ne lui appartient pas.(3) Prenons E = F =1, 2, 3, 4, et la relation sur E «x + y est divisible par 3». Le graphe contient cinq éléments, qui sont:
du couple (x , y ). Lorsque F = E, on dit qu’on a une relation sur E. Si une relation 倫 est vraie pour le couple (x , y ), on écrira souvent x 倫 y .Exemples(1) Sur un ensemble E, la relation d’égalité «x = y » a pour graphe l’ensemble des couples (x , x), x 捻 E; cet ensemble est appelé la diagonale de l’ensemble E 憐 E.(2) Prenons pour E l’ensemble des quatre voyellesa , e , i , o et pour F l’ensemble des quatre premiers chiffres1, 2, 3, 4; la figure 16 indique les représentations cartésienne et sagittale de la relation «la voyelle x figure dans l’écriture en langue française du chiffre y ». Par exemple (a , 4) appartient au graphe (car a est dans qua tre), mais (a , 3) ne lui appartient pas.(3) Prenons E = F =1, 2, 3, 4, et la relation sur E «x + y est divisible par 3». Le graphe contient cinq éléments, qui sont: la figure 17 donne la représentation sagittale de ce graphe: remarquer la boucle pour représenter (3, 3).(4) Sur l’ensemble R des nombres réels, soit la relation «x 諒 y ». Si on identifie, comme indiqué ci-dessus, l’ensemble des couples de nombres réels aux points du plan, le graphe est constitué des points de la première bissectrice y = x et des points situés au-dessus de cette droite (fig. 18).(5) Toujours sur R, considérons maintenant la relation «|x 漣 y | 麗 1». Son graphe est ici la bande du plan comprise entre les deux droites x 漣 y = 1 et x 漣 y = 漣 1 (fig. 18).(6) Encore sur R, soit la relation «x 漣 y est un entier relatif»; le graphe de cette relation est le sous-ensemble du plan formé des droites y = x + n , lorsque n parcourt l’ensemble des entiers relatifs (fig. 18).Propriétés des relationsOn se limite maintenant à des relations sur un ensemble E et on se propose de dégager un certain nombre de propriétés de ces relations.Une relation sur E est dite réflexive si, pour tout élément x 捻 E, la relation est vraie pour le couple (x , x ); cela revient donc à dire que tous les couples (x , x ) appartiennent au graphe de la relation, ou encore que ce graphe contient la diagonale de l’ensemble E 憐 E. Les relations données ci-dessus sont réflexives dans les exemples (1), (4), (5), (6), non réflexives dans l’exemple (3).Une relation sur E est dite symétrique si, toutes les fois que la relation est vraie pour un couple (x , y ), elle est aussi vraie pour le couple (y , x ). Ainsi les relations des exemples (1), (3), (5), (6) sont symétriques, celle de l’exemple (4) ne l’est pas. À l’opposé, une relation est dite antisymétrique si on a nécessairement x = y quand la relation est vraie à la fois pour le couple (x , y ) et pour le couple (y , x ); c’est le cas de (4).Une relation sur E est dite transitive si, toutes les fois que la relation est vraie pour des couples (x , y ) et (y , z ), elle est aussi vraie pour le couple (x , z ). Ainsi, les relations des exemples (1), (4), (6) sont transitives, celles des exemples (3) et (5) ne le sont pas: ainsi, dans l’exemple (3), la relation est vraie pour les couples (1, 2) et (2, 4), mais ne l’est pas pour le couple (1, 4).Avec ces notions, on peut désormais distinguer différents types de relations. Les relations d’ordre sont les relations qui, comme dans l’exemple (4), sont réflexives, antisymétriques et transitives; ces relations sont très importantes, mais nous ne les étudierons pas ici, et nous renvoyons à l’article ensembles ORDONNÉS. Les relations d’équivalence sont celles qui, comme dans l’exemple (6), sont réflexives, symétriques et transitives (cf. infra , Relations d’équivalence ).Applications d’un ensemble dans un autreDéfinitionsOn revient à la situation générale de deux ensembles E et F et d’une relation de source E et de but F.Nous dirons qu’une relation de source E et de but F est une application de E dans F si, pour tout élément x 捻 E, il existe un unique élément y 捻 F tel que la relation soit vraie pour (x , y ). Ainsi à tout élément x 捻 E correspond un unique élément y 捻 F appelé l’image de x par l’application. Si l’application est désignée par f , on notera y = f (x ) l’image de x ; on écrira:
la figure 17 donne la représentation sagittale de ce graphe: remarquer la boucle pour représenter (3, 3).(4) Sur l’ensemble R des nombres réels, soit la relation «x 諒 y ». Si on identifie, comme indiqué ci-dessus, l’ensemble des couples de nombres réels aux points du plan, le graphe est constitué des points de la première bissectrice y = x et des points situés au-dessus de cette droite (fig. 18).(5) Toujours sur R, considérons maintenant la relation «|x 漣 y | 麗 1». Son graphe est ici la bande du plan comprise entre les deux droites x 漣 y = 1 et x 漣 y = 漣 1 (fig. 18).(6) Encore sur R, soit la relation «x 漣 y est un entier relatif»; le graphe de cette relation est le sous-ensemble du plan formé des droites y = x + n , lorsque n parcourt l’ensemble des entiers relatifs (fig. 18).Propriétés des relationsOn se limite maintenant à des relations sur un ensemble E et on se propose de dégager un certain nombre de propriétés de ces relations.Une relation sur E est dite réflexive si, pour tout élément x 捻 E, la relation est vraie pour le couple (x , x ); cela revient donc à dire que tous les couples (x , x ) appartiennent au graphe de la relation, ou encore que ce graphe contient la diagonale de l’ensemble E 憐 E. Les relations données ci-dessus sont réflexives dans les exemples (1), (4), (5), (6), non réflexives dans l’exemple (3).Une relation sur E est dite symétrique si, toutes les fois que la relation est vraie pour un couple (x , y ), elle est aussi vraie pour le couple (y , x ). Ainsi les relations des exemples (1), (3), (5), (6) sont symétriques, celle de l’exemple (4) ne l’est pas. À l’opposé, une relation est dite antisymétrique si on a nécessairement x = y quand la relation est vraie à la fois pour le couple (x , y ) et pour le couple (y , x ); c’est le cas de (4).Une relation sur E est dite transitive si, toutes les fois que la relation est vraie pour des couples (x , y ) et (y , z ), elle est aussi vraie pour le couple (x , z ). Ainsi, les relations des exemples (1), (4), (6) sont transitives, celles des exemples (3) et (5) ne le sont pas: ainsi, dans l’exemple (3), la relation est vraie pour les couples (1, 2) et (2, 4), mais ne l’est pas pour le couple (1, 4).Avec ces notions, on peut désormais distinguer différents types de relations. Les relations d’ordre sont les relations qui, comme dans l’exemple (4), sont réflexives, antisymétriques et transitives; ces relations sont très importantes, mais nous ne les étudierons pas ici, et nous renvoyons à l’article ensembles ORDONNÉS. Les relations d’équivalence sont celles qui, comme dans l’exemple (6), sont réflexives, symétriques et transitives (cf. infra , Relations d’équivalence ).Applications d’un ensemble dans un autreDéfinitionsOn revient à la situation générale de deux ensembles E et F et d’une relation de source E et de but F.Nous dirons qu’une relation de source E et de but F est une application de E dans F si, pour tout élément x 捻 E, il existe un unique élément y 捻 F tel que la relation soit vraie pour (x , y ). Ainsi à tout élément x 捻 E correspond un unique élément y 捻 F appelé l’image de x par l’application. Si l’application est désignée par f , on notera y = f (x ) l’image de x ; on écrira: pour exprimer que f est une application de E dans F, et:
pour exprimer que f est une application de E dans F, et: pour exprimer que y est l’image de x par f. Si E et F sont des ensembles finis, la flèche de la représentation sagittale représente le passage de x à son image f (x ).La relation d’égalité sur un ensemble E donne un exemple trivial d’application; l’image de tout élément x 捻 E est cet élément x lui-même. On obtient ainsi ce qu’on appelle l’application identique de E dans lui-même, notée 1E.On introduit aussi souvent, non sans quelques confusions, la notion de relation fonctionnelle, ou de fonction. Une relation de source E et de but F est une fonction si, pour tout élément x 捻 E, il existe au plus un élément y 捻 F pour lequel la relation est vraie. On appelle alors ensemble de définition d’une telle fonction le sous-ensemble E de E formé des éléments x 捻 E pour lesquels il existe effectivement un tel y ; si on fait correspondre à tout élément x 捻 E cet élément y 捻 F, on définit une application de E dans F, mais il est fondamental, si E E, de ne pas confondre la fonction initiale de l’application que nous venons de lui associer, car la première relation est de source E et la seconde de source E . Par exemple, considérons sur R la relation:
pour exprimer que y est l’image de x par f. Si E et F sont des ensembles finis, la flèche de la représentation sagittale représente le passage de x à son image f (x ).La relation d’égalité sur un ensemble E donne un exemple trivial d’application; l’image de tout élément x 捻 E est cet élément x lui-même. On obtient ainsi ce qu’on appelle l’application identique de E dans lui-même, notée 1E.On introduit aussi souvent, non sans quelques confusions, la notion de relation fonctionnelle, ou de fonction. Une relation de source E et de but F est une fonction si, pour tout élément x 捻 E, il existe au plus un élément y 捻 F pour lequel la relation est vraie. On appelle alors ensemble de définition d’une telle fonction le sous-ensemble E de E formé des éléments x 捻 E pour lesquels il existe effectivement un tel y ; si on fait correspondre à tout élément x 捻 E cet élément y 捻 F, on définit une application de E dans F, mais il est fondamental, si E E, de ne pas confondre la fonction initiale de l’application que nous venons de lui associer, car la première relation est de source E et la seconde de source E . Par exemple, considérons sur R la relation: c’est une fonction dont le domaine de définition est l’ensemble E des nombres réels différents de 1 et elle définit une application f : E R telle que:
c’est une fonction dont le domaine de définition est l’ensemble E des nombres réels différents de 1 et elle définit une application f : E R telle que: Si f : EF est une application de E dans F, on appelle graphe de f son graphe au sens général défini ci-dessus pour une relation. C’est le sous-ensemble de E 憐 F formé des couples (x , f (x )), x 捻 E; ainsi, si G est ce graphe:
Si f : EF est une application de E dans F, on appelle graphe de f son graphe au sens général défini ci-dessus pour une relation. C’est le sous-ensemble de E 憐 F formé des couples (x , f (x )), x 捻 E; ainsi, si G est ce graphe: Dans le cas où E 說 R et F = R, le graphe est le sous-ensemble de R2 formé des couples (x , y ) tels que x 捻 E et y = f (x ); c’est le graphe, au sens usuel, de f .Composition des applicationsSoit f : EF et g : FG deux applications; remarquons ce qui est essentiel ici, que l’ensemble source de g est le même que l’ensemble but de f . Considérons la propriété suivante des couples (x , z ) 捻 E 憐 G: il existe un élément y 捻 F tel que y = f (x ) et z =g (y ); cette relation sur E 憐 G est en fait une application de E dans G. En effet, pour x 捻 E donné, l’élément y = f (x ) est parfaitement déterminé, et la relation exprime que z = g (f (x )). Ainsi, à tout x 捻 E cette application, appelée application composée de f et g et notée g 獵 f (dans cet ordre) fait correspondre à x l’unique élément z imagepar g de l’élément y = f (x ). Pratiquement, pour trouver l’image par g 獵 f d’un élément x 捻 E, on cherche donc d’abord l’image y de x par f , puis l’image par g de cet élément y .Soit par exemple les ensembles E =a, b , c, F = 見, 廓, 塚, 嗀 et G =1, 2, 3; considérons f : EF et g : FG telles que:
Dans le cas où E 說 R et F = R, le graphe est le sous-ensemble de R2 formé des couples (x , y ) tels que x 捻 E et y = f (x ); c’est le graphe, au sens usuel, de f .Composition des applicationsSoit f : EF et g : FG deux applications; remarquons ce qui est essentiel ici, que l’ensemble source de g est le même que l’ensemble but de f . Considérons la propriété suivante des couples (x , z ) 捻 E 憐 G: il existe un élément y 捻 F tel que y = f (x ) et z =g (y ); cette relation sur E 憐 G est en fait une application de E dans G. En effet, pour x 捻 E donné, l’élément y = f (x ) est parfaitement déterminé, et la relation exprime que z = g (f (x )). Ainsi, à tout x 捻 E cette application, appelée application composée de f et g et notée g 獵 f (dans cet ordre) fait correspondre à x l’unique élément z imagepar g de l’élément y = f (x ). Pratiquement, pour trouver l’image par g 獵 f d’un élément x 捻 E, on cherche donc d’abord l’image y de x par f , puis l’image par g de cet élément y .Soit par exemple les ensembles E =a, b , c, F = 見, 廓, 塚, 嗀 et G =1, 2, 3; considérons f : EF et g : FG telles que: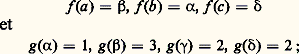
 (la figure 19 représente les diagrammes sagittaux des graphes de ces applications).Avec E = F = G = R, voici un autre exemple. Soit f : RR et g : RR définies par f (x ) = x 2 et g (x ) = 2x + 1; ici on peut composer f et g , mais aussi g et f . Ces deux applications de R dans R sont définies par g 獵 f (x ) = 2x 2 + 1 et f 獵 g (x ) = (2x + 1)2; il s’agit d’applications distinctes.Propriétés des applicationsUne application f : EF est dite surjective si, pour tout élément y 捻 F, il existe au moins un élément x 捻 E ayant pour image y , c’est-à-dire tel que y = f (x ); on dit souvent que f est une application de E sur F, ou est une surjection. Ainsi, dans le premier exemple donné ci-dessus (cf. «Composition des applications»), l’application g est surjective ainsi que l’application g 獵 f ; l’application f , au contraire, ne l’est pas, car il n’existe aucun élément de E ayant pour image 塚.Une application f : EF est dite injective si, pour tout élément y 捻 F, il existe au plus un élément x 捻 E ayant pour image y ; cela revient à dire que deux éléments distincts de E ont des images qui sont des éléments distincts de F. On dit souvent que f est une injection de E dans F. Ainsi, toujours en reprenant le premier exemple donné dans «Composition des applications», les applications f et g 獵 f sont injectives, tandis que g ne l’est pas (en effet, 塚 et 嗀 ont même image par l’application g ).Attirons l’attention ici sur l’importance, pour définir une application, de préciser les ensembles source et but. Ainsi, désignant par R+ l’ensemble des nombres réels positifs, considérons les trois applications:
(la figure 19 représente les diagrammes sagittaux des graphes de ces applications).Avec E = F = G = R, voici un autre exemple. Soit f : RR et g : RR définies par f (x ) = x 2 et g (x ) = 2x + 1; ici on peut composer f et g , mais aussi g et f . Ces deux applications de R dans R sont définies par g 獵 f (x ) = 2x 2 + 1 et f 獵 g (x ) = (2x + 1)2; il s’agit d’applications distinctes.Propriétés des applicationsUne application f : EF est dite surjective si, pour tout élément y 捻 F, il existe au moins un élément x 捻 E ayant pour image y , c’est-à-dire tel que y = f (x ); on dit souvent que f est une application de E sur F, ou est une surjection. Ainsi, dans le premier exemple donné ci-dessus (cf. «Composition des applications»), l’application g est surjective ainsi que l’application g 獵 f ; l’application f , au contraire, ne l’est pas, car il n’existe aucun élément de E ayant pour image 塚.Une application f : EF est dite injective si, pour tout élément y 捻 F, il existe au plus un élément x 捻 E ayant pour image y ; cela revient à dire que deux éléments distincts de E ont des images qui sont des éléments distincts de F. On dit souvent que f est une injection de E dans F. Ainsi, toujours en reprenant le premier exemple donné dans «Composition des applications», les applications f et g 獵 f sont injectives, tandis que g ne l’est pas (en effet, 塚 et 嗀 ont même image par l’application g ).Attirons l’attention ici sur l’importance, pour définir une application, de préciser les ensembles source et but. Ainsi, désignant par R+ l’ensemble des nombres réels positifs, considérons les trois applications: ces trois applications sont distinctes et possèdent des propriétés différentes: f n’est ni injective ni surjective, g est surjective, mais n’est pas injective, et h est injective, mais n’est pas surjective.BijectionsUne application f : EF qui est à la fois injective et surjective est dite bijective ; on dit aussi que f est une bijection. Les bijections jouent un rôle très important en théorie des ensembles (construction des cardinaux par exemple: cf. INFINI MATHÉMATIQUE); du point de vue de la théorie des ensembles proprement dite, on peut «identifier» des ensembles E et F tels qu’il existe une bijection de E sur F (ce que avons fait plus haut pour le plan et R 憐 R).Si f : EF est une bijection, pour tout élément y 捻 F il existe un unique élément x 捻 E tel que y = f (x ); la propriété du couple (u , v ) 捻 F 憐 E:
ces trois applications sont distinctes et possèdent des propriétés différentes: f n’est ni injective ni surjective, g est surjective, mais n’est pas injective, et h est injective, mais n’est pas surjective.BijectionsUne application f : EF qui est à la fois injective et surjective est dite bijective ; on dit aussi que f est une bijection. Les bijections jouent un rôle très important en théorie des ensembles (construction des cardinaux par exemple: cf. INFINI MATHÉMATIQUE); du point de vue de la théorie des ensembles proprement dite, on peut «identifier» des ensembles E et F tels qu’il existe une bijection de E sur F (ce que avons fait plus haut pour le plan et R 憐 R).Si f : EF est une bijection, pour tout élément y 捻 F il existe un unique élément x 捻 E tel que y = f (x ); la propriété du couple (u , v ) 捻 F 憐 E: est une relation sur F 憐 E qui est en fait une bijection de F sur E. En effet, puisque f est une bijection, pour tout u 捻 F il existe un unique élément v 捻 E ayant pour image u ; la bijection ainsi définie est appelée la bijection réciproque de la bijection f , notée f -1. C’est donc une application de F dans E, et on a la caractérisation:
est une relation sur F 憐 E qui est en fait une bijection de F sur E. En effet, puisque f est une bijection, pour tout u 捻 F il existe un unique élément v 捻 E ayant pour image u ; la bijection ainsi définie est appelée la bijection réciproque de la bijection f , notée f -1. C’est donc une application de F dans E, et on a la caractérisation: On disait autrefois que f ou f -1 établissaient une correspondance biunivoque entre E et F; en effet, les formules précédentes associent deux à deux les éléments de E et ceux de F. Remarquons que l’on peut composer f -1 獵 f et f 獵 f -1; on obtient ainsi respectivement les applications identiques (c’est-à-dire la relation d’égalité) dans E et F respectivement.Dans le premier exemple du paragraphe «Composition des applications», l’application g 獵 f est une bijection de E =a , b , c sur G =1, 2, 3; l’application réciproque serait:
On disait autrefois que f ou f -1 établissaient une correspondance biunivoque entre E et F; en effet, les formules précédentes associent deux à deux les éléments de E et ceux de F. Remarquons que l’on peut composer f -1 獵 f et f 獵 f -1; on obtient ainsi respectivement les applications identiques (c’est-à-dire la relation d’égalité) dans E et F respectivement.Dans le premier exemple du paragraphe «Composition des applications», l’application g 獵 f est une bijection de E =a , b , c sur G =1, 2, 3; l’application réciproque serait: Relations d’équivalenceOn appelle relation d’équivalence sur un ensemble E une relation sur E qui est réflexive, symétrique et transitive. Si une relation d’équivalence donnée est vraie pour un couple (x , y ), on dit que ces éléments sont équivalents (modulo la relation considérée) et on note x 黎 y .Exemples(1) Sur l’ensemble E =1, 2, 3, 4, considérons la relation «x 漣 y est un multiple de 3» (dans les entiers relatifs). On vérifie facilement que c’est une relation d’équivalence; la figure 20 représente le diagramme sagittal de cette relation.(2) Voici un exemple plus général (en fait, toutes les relations d’équivalence peuvent être obtenues ainsi). Soit f : EF une application d’un ensemble E dans un ensemble F. La relation sur E:
Relations d’équivalenceOn appelle relation d’équivalence sur un ensemble E une relation sur E qui est réflexive, symétrique et transitive. Si une relation d’équivalence donnée est vraie pour un couple (x , y ), on dit que ces éléments sont équivalents (modulo la relation considérée) et on note x 黎 y .Exemples(1) Sur l’ensemble E =1, 2, 3, 4, considérons la relation «x 漣 y est un multiple de 3» (dans les entiers relatifs). On vérifie facilement que c’est une relation d’équivalence; la figure 20 représente le diagramme sagittal de cette relation.(2) Voici un exemple plus général (en fait, toutes les relations d’équivalence peuvent être obtenues ainsi). Soit f : EF une application d’un ensemble E dans un ensemble F. La relation sur E: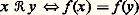 est une relation d’équivalence dite associée à l’application f. (3) La donnée d’une «fraction» p /q équivaut à la donnée de son numérateur p , qui est un entier relatif quelconque, et de son dénominateur, qui est un entier relatif non nul , c’est-à-dire qu’elle équivaut à la donnée du couple (p , q ), p 捻 Z et q 捻 Z = Z 漣0. Dans ce qui suit, nous identifierons donc l’ensemble des fractions à l’ensemble produit Z 憐 Z. Sur cet ensemble, la relation:
est une relation d’équivalence dite associée à l’application f. (3) La donnée d’une «fraction» p /q équivaut à la donnée de son numérateur p , qui est un entier relatif quelconque, et de son dénominateur, qui est un entier relatif non nul , c’est-à-dire qu’elle équivaut à la donnée du couple (p , q ), p 捻 Z et q 捻 Z = Z 漣0. Dans ce qui suit, nous identifierons donc l’ensemble des fractions à l’ensemble produit Z 憐 Z. Sur cet ensemble, la relation: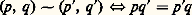 (le produit des «extrêmes» est égal au produit des «moyens») est une relation d’équivalence.(4) Sur l’ensemble des droites du plan, la relation D//D , qui exprime que les droites D et D sont parallèles ou confondues, est une relation d’équivalence.(5) Sur l’ensemble des «vecteurs» du plan, c’est-à-dire des couples de points du plan (origine, extrémité), la relation d’équipollence «AB黎 CDsi les segments AD et BC ont même milieu» est une relation d’équivalence.Ensemble quotientSoit E un ensemble muni d’une relation d’équivalence. Pour tout élément x 捻 E, on appelle classe d’équivalence de x l’ensemble, noté Cx ou face="EU Updot" 來 , des éléments de E qui sont équivalents à x ; c’est le sous-ensemble de E:
(le produit des «extrêmes» est égal au produit des «moyens») est une relation d’équivalence.(4) Sur l’ensemble des droites du plan, la relation D//D , qui exprime que les droites D et D sont parallèles ou confondues, est une relation d’équivalence.(5) Sur l’ensemble des «vecteurs» du plan, c’est-à-dire des couples de points du plan (origine, extrémité), la relation d’équipollence «AB黎 CDsi les segments AD et BC ont même milieu» est une relation d’équivalence.Ensemble quotientSoit E un ensemble muni d’une relation d’équivalence. Pour tout élément x 捻 E, on appelle classe d’équivalence de x l’ensemble, noté Cx ou face="EU Updot" 來 , des éléments de E qui sont équivalents à x ; c’est le sous-ensemble de E: Remarquons que tous les éléments d’une même classe d’équivalence sont équivalents entre eux et que deux éléments équivalents ont des classes égales (symétrie et transitivité de la relation d’équivalence). Il en résulte que si deux éléments x et y ne sont pas équivalents, leurs classes d’équivalence sont disjointes, c’est-à-dire n’ont pas d’élément commun.Puisque les classes d’équivalence sont des sous-ensembles de E, l’ensemble de ces classes d’équivalence est un sous-ensemble de l’ensemble 戮 (E) des parties de E; on appelle ensemble quotient de E par la relation d’équivalence considérée ce sous-ensemble de 戮 (E), qui admet pour éléments les classes d’équivalence. Remarquons que l’ensemble quotient est une partition de l’ensemble E: les classes d’équivalence sont toutes non vides, et tout élément de E appartient à une classe d’équivalence et une seule, la sienne (et celle de tous les éléments qui lui sont équivalents). Réciproquement, si 杻 說 戮(E) est une partition, on peut lui associer la relation d’équivalence: «x et y appartiennent au même sous-ensemble de la partition»; bien entendu, on retrouve comme ensemble quotient par cette relation d’équivalence la partition initiale, la classe d’un élément étant ici l’unique ensemble de la partition auquel il appartient.Reprenons, avec ces nouvelles notions, les exemples que l’on vient de donner. Dans l’exemple (1), on a:
Remarquons que tous les éléments d’une même classe d’équivalence sont équivalents entre eux et que deux éléments équivalents ont des classes égales (symétrie et transitivité de la relation d’équivalence). Il en résulte que si deux éléments x et y ne sont pas équivalents, leurs classes d’équivalence sont disjointes, c’est-à-dire n’ont pas d’élément commun.Puisque les classes d’équivalence sont des sous-ensembles de E, l’ensemble de ces classes d’équivalence est un sous-ensemble de l’ensemble 戮 (E) des parties de E; on appelle ensemble quotient de E par la relation d’équivalence considérée ce sous-ensemble de 戮 (E), qui admet pour éléments les classes d’équivalence. Remarquons que l’ensemble quotient est une partition de l’ensemble E: les classes d’équivalence sont toutes non vides, et tout élément de E appartient à une classe d’équivalence et une seule, la sienne (et celle de tous les éléments qui lui sont équivalents). Réciproquement, si 杻 說 戮(E) est une partition, on peut lui associer la relation d’équivalence: «x et y appartiennent au même sous-ensemble de la partition»; bien entendu, on retrouve comme ensemble quotient par cette relation d’équivalence la partition initiale, la classe d’un élément étant ici l’unique ensemble de la partition auquel il appartient.Reprenons, avec ces nouvelles notions, les exemples que l’on vient de donner. Dans l’exemple (1), on a: ainsi l’ensemble quotient contient trois éléments, qui sont1, 4,2, 5 et3. Les exemples (3) à (5) montrent comment une relation d’équivalence permet de définir de nouveaux objets mathématiques. Dans (3), toutes les fractions équivalentes entre elles correspondent au même nombre rationnel; par définition , on appellera nombre rationnel tout élément de l’ensemble quotient: on a ici une construction mathématique rigoureuse des nombres rationnels à partir des entiers relatifs. Les exemples (4) et (5) permettraient de définir mathématiquement les notions de direction de droite et de vecteur libre respectivement.ReprésentantsSi C est un élément de l’ensemble quotient, on appelle représentant de cette classe tout élément x 捻 C, c’est-à-dire tout élément de E tel que Cx = C. Comme il est souvent plus facile de manipuler les éléments de E que les éléments de l’ensemble quotient, il est intéressant de trouver des représentants de toutes les classes d’équivalence, «sans omission ni répétition». Un sous-ensemble S de E est appelé un système complet de représentants si tout élément de E est équivalent à un élément de S et à un seul. Ainsi, dans l’exemple (1) ci-dessus, on peut prendre S =1, 2, 3.Examinons l’exemple (2). Une fraction p/q sera dite irréductible si q 礪 0 et si p et q sont premiers entre eux. Les propriétés élémentaires des entiers montrent que chaque classe d’équivalence contient une fraction irréductible et une seule, toutes les fractions équivalentes étant de la forme kp/kq , k 捻 Z; ainsi, les fractions irréductibles forment un système complet de représentants des nombres rationnels.Dans l’exemple (5), fixons un point O du plan; dans chaque vecteur libre, il existe un vecteur et un seul d’origine O (ce qu’on exprime dans le langage usuel en disant que le choix de son origine détermine complètement un vecteur libre); ainsi les vecteurs d’origine O forment un système complet de représentants des vecteurs libres du plan.
ainsi l’ensemble quotient contient trois éléments, qui sont1, 4,2, 5 et3. Les exemples (3) à (5) montrent comment une relation d’équivalence permet de définir de nouveaux objets mathématiques. Dans (3), toutes les fractions équivalentes entre elles correspondent au même nombre rationnel; par définition , on appellera nombre rationnel tout élément de l’ensemble quotient: on a ici une construction mathématique rigoureuse des nombres rationnels à partir des entiers relatifs. Les exemples (4) et (5) permettraient de définir mathématiquement les notions de direction de droite et de vecteur libre respectivement.ReprésentantsSi C est un élément de l’ensemble quotient, on appelle représentant de cette classe tout élément x 捻 C, c’est-à-dire tout élément de E tel que Cx = C. Comme il est souvent plus facile de manipuler les éléments de E que les éléments de l’ensemble quotient, il est intéressant de trouver des représentants de toutes les classes d’équivalence, «sans omission ni répétition». Un sous-ensemble S de E est appelé un système complet de représentants si tout élément de E est équivalent à un élément de S et à un seul. Ainsi, dans l’exemple (1) ci-dessus, on peut prendre S =1, 2, 3.Examinons l’exemple (2). Une fraction p/q sera dite irréductible si q 礪 0 et si p et q sont premiers entre eux. Les propriétés élémentaires des entiers montrent que chaque classe d’équivalence contient une fraction irréductible et une seule, toutes les fractions équivalentes étant de la forme kp/kq , k 捻 Z; ainsi, les fractions irréductibles forment un système complet de représentants des nombres rationnels.Dans l’exemple (5), fixons un point O du plan; dans chaque vecteur libre, il existe un vecteur et un seul d’origine O (ce qu’on exprime dans le langage usuel en disant que le choix de son origine détermine complètement un vecteur libre); ainsi les vecteurs d’origine O forment un système complet de représentants des vecteurs libres du plan.
Encyclopédie Universelle. 2012.
